1.6 Equazioni e disequazioni algebriche
Si definiscono equazioni delle uguaglianze fra espressioni matematiche in cui compaiono una o più incognite. Cercare le soluzioni dell’equazione vuol dire trovare quei valori numerici che, sostituiti alle incognite, rendono vera l’uguaglianza. Vediamo subito un esempio!
es. : x-1=0 —> x=1
x è l’incognita; x=1 è la soluzione dell’equazione
In generale esistono due diversi tipi di equazioni:
- Numerica intera -> l’incognita non figura al denominatore (es. 3x + 4 = 5x)
- Numerica fratta -> l’incognita figura al denominatore (es. 3/(7+x) = 2x/(x-1))
In particolare, possiamo caratterizzare le equazioni al variare dei propri termini, ovvero:
Un’equazione è in forma normale se il polinomio, nella variabile x, non contiene termini simili. (es. 3x + x^2 = 1)
Un’equazione si dice lineare se è di primo grado. (es. 3x + 7x – 3 = 1 – 2x) Un’equazione si dice determinata se ha un numero finito di soluzioni. (es. risolvendo l’eq di cui sopra: 10x + 2x = 1 + 3 -> 8x = 4 -> x = 1/2)
Un’equazione si dice indeterminata se ha infinite soluzioni (es. 0x = 0; qualsiasi numero moltiplicato per 0 dà 0)
Un’equazione si dice impossibile se non ammette soluzioni (es. 3x^2 = -1; nessun numero elevato al quadrato e moltiplicato per un numero positivo, in questo caso 3, dà un numero negativo)
A questo punto, passiamo alle operazioni che consentono di svolgere in passaggi più o meno rapidi una data equazione; sappiamo che, se si addiziona (o si sottrae) ai due membri di un’equazione uno stesso numero o una stessa espressione, si ottiene un’equazione equivalente: abbiamo enunciato, dunque,il Primo Principio di Equivalenza. (es. : x+4=9 e x-5=0 sono equazioni equivalenti (si è sottratto 9 a dx e sx))
In generale esistono due regole per la risoluzione delle equazioni:
- regola del trasporto: è possibile spostare un termine da un membro all’altro, purché lo si cambi di segno.
es. : x+4=9. ——-> x=9-4 ——> x=5 (si è spostato il 4 da sx a dx cambiandogli il segno)
- E’ possibile eliminare dai due membri due termini uguali
es. : 2x-4+2=x+2 –> 2x – 4 = x (si è rimosso a dx e sx il ‘+2’)
Il Secondo Principio di Equivalenza, invece, afferma che: data un’equazione, se si moltiplicano o si dividono i due membri per uno stesso numero o una stessa espressione, purchè diversi da 0, si ottiene un’equazione equivalente. (es. : 3x=5 è equivalente a 3x/3= 5/3 —-> x=5/3 (si è diviso per 3 a dx e sx))
Dal secondo principio derivano due regole:
- divisione per un fattore comune: se tutti i termini di un’equazione hanno un fattore numerico comune, si possono dividere tutti i termini per tale fattore (3x + 6 = -3 +12x -> tutti i termini hanno fattore 3 in comune -> dividiamo tutto per 3 -> x + 2 = – 1 +4x)
- cambiamento di segno: moltiplicando entrambi i membri di un’equazione per -1 è possibile cambiare segno a tutti i termini. (es. 2x – 1 = -1 – 3x -> moltiplicando per ‘-1’ diventa: -2x + 1 = 1 + 3x)
Finora abbiamo analizzato principalmente equazioni di primo grado, ovvero l’esponente dell’incognita era di grado 1; ma, nel caso di un’equazione di secondo grado (es. con x^2 per intenderci), essa è comunque riconducibile alla forma normale, cioè:
ax^2 + bx +c =0, con a≠0 e a,b,c numeri reali
Sono presenti: un termine di secondo grado (ax^2 ), uno di primo grado (bx) e un termine noto (c).
- se entrambi i coefficienti b e c sono diversi da 0, l’equazione si dice completa (es. 3x^2 – 2x -1=0)
- si dice spuria se b ≠ 0 e c = 0 (es. x^2 -2x=0), pura se b = 0 e c ≠ 0 (es. x^2 -1=0), monomia se b = 0 e c = 0 (es. 3x^2=0).
Dato il trinomio ax^2 + bx + c , se l’equazione associata ax^2 + bx + c = 0 ha soluzioni reali, tali soluzioni ( x1 e x 2 ) sono anche zeri del trinomio.
Il trinomio è:
- scomponibile in fattori se (date x1 e x2 soluzioni)
Δ = b^2-4ac >0, cioè ax^2 + bx + c =a*(x−x1)*(x−x2) (x1 e x2 non sono coincidenti)
(es. x^2-5x+4 -> Δ = b^2-4ac = 25-16=9 -> x1,2 = (5+-3/2) -> x1 = 4, x2 = 1 -> si scrive (x-4)(x-1) = x^2 -5x +4)
Δ = b^2-4ac = 0, cioè ax^2 + bx + c = a*(x − x1)^2 (x1 e x2 sono coincidenti)
(es. x^2-2x+1 -> Δ = b^2-4ac = 4-4 =0 -> x1,2 = (2+-0/2) -> x1 = x2 = 1 -> si scrive (x-1)^2 = x^2 -2x +1)
- irriducibile in R se Δ < 0 (es. x^2+4x+5 -> Δ = b^2-4ac = 16-20=-4 <0)
Esiste, però, un’altra tipologia di equazioni, le cosiddette equazioni irrazionali, ovvero quelle contenenti almeno un radicale nel cui radicando compare l’incognita. Se l’equazione è risolvibile: per indice della radice pari, abbiamo due soluzioni; per indice della radice dispari, abbiamo un’unica soluzione.
In figura è presente un esempio svolto:
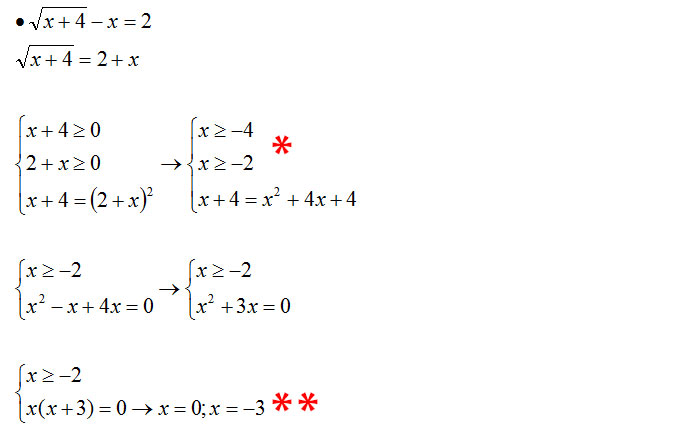
©Esercizimatematica
Dunque, innanzitutto si isola la radice quadrata, e si spostano tutti i restanti membri alla dx dell’equazione; dopodichè si svolge un sistema in cui compaiono necessariamente le condizioni di esistenza (ovvero tutto quello che è sotto la radice dev’essere maggiore o uguale di 0, e idem l’intero membro a dx dell’equazione) e l’equazione vera e propria in cui si eleva all’indice n sia il membro di dx che di sx (nel caso in particolare si è elevato per 2 perchè vi era una radice quadrata); si risolve l’equazione di secondo grado e si ottengono 2 soluzioni: esse saranno compatibili, o anche una di esse, solo se rispetteranno la condizione di esistenza calcolata, e pertanto saranno soluzioni dell’equazione irrazionale (nel caso in esame’Dunque, innanzitutto si isola la radice quadrata, e si spostano tutti i restanti membri alla dx dell’equazione; dopodichè si svolge un sistema in cui compaiono necessariamente le condizioni di esistenza (ovvero tutto quello che è sotto la radice dev’essere maggiore o uguale di 0, e idem l’intero membro a dx dell’equazione) e l’equazione vera e propria in cui si eleva all’indice n sia il membro di dx che di sx (nel caso in particolare si è elevato per 2 perchè vi era una radice quadrata); si risolve l’equazione di secondo grado e si ottengono 2 soluzioni: esse saranno compatibili, o anche una di esse, solo se rispetteranno la condizione di esistenza calcolata, e pertanto saranno soluzioni dell’equazione irrazionale (nel caso in esame solo 0 è soluzione dell’equazione, perchè è maggiore di -2, a differenza di -3, che non rispetta la condiz. di esistenza e dunque non è una soluzione ammissibile)
Come abbiamo potuto constatare anche e proprio nell’esempio precedente, le equazioni sono strettamente correlate alle disequazioni (e viceversa), ovvero delle disuguaglianze fra espressioni numerico-letterali; il procedimento è analogo a quello esposto precedentemente ma in tal caso si parla di intervalli di valore in cui ricadono le soluzioni. Gli intervalli si distinguono in:
Limitati:
- Intervallo aperto ]a; b[
- Intervallo chiuso [a; b]
- Intervallo aperto a destra [a; b[
- Intervallo aperto a sinistra ]a; b]
Illimitati:
- Intervallo aperto illimitato superiormente ]a;+∞[
- Intervallo aperto illimitato inferiormente ]−∞ ; a[
- Intervallo chiuso illimitato superiormente [a;+∞[
- Intervallo chiuso illimitato inferiormente ]−∞ ; a].
Anche in questo caso, analogamente a quanto fatto precedentemente (con la differenza che al simbolo dell’uguale si sostituiscono > e <), possiamo enunciare i Princìpi di equivalenza, cioè:
data una disequazione, si ottiene una disequazione a essa equivalente:
• aggiungendo a entrambi i membri uno stesso numero (o espressione);
• moltiplicando o dividendo entrambi i membri per uno stesso numero (o espressione) positivo;
• moltiplicando o dividendo entrambi i membri per uno stesso numero (o espressione) negativo e cambiando il verso della disuguaglianza.
Anche nel caso delle disequazioni abbiamo quelle fratte; per risolvere una disequazione fratta del tipo:
A(x)/ B(x) >0, posto B(x)≠0, dobbiamo studiare il segno della frazione A(x)/B(x)
(es. (3x+1)/(-2x+2)>0 ; c.e. x diverso da 1-> N: 3x+1 >0 -> x > -1/3 ; D: -2x+2 >0 -> x < 1
–> -1/3 //// 1
N – //// + //// +
D + //// + //// –
Dunque, la frazione risulta positiva solo per x compresa tra -1/3 e 1 -> -1/3<x<1.
Inoltre, come visto per le equazioni, vi sono anche le disequazioni irrazionali; in figura è presente il criterio di svolgimento nelle varie casistiche di questo tipo di equazioni (A(x) rappresenta il polinomio sotto la radice mentre B(x) rappresenta il membro a dx dell’equazione):

©Eduboom
In figura si può osservare un esempio di diseq. irrazionale con indice pari e segno ‘>’:

©Slideserve
Un’altra categoria di equazioni/disequazioni è quella delle eq./diseq. in valore assoluto, ovvero l’incognita è contenuta anche nel valore assoluto; in tal caso si esamina il segno di ogni espressione che sia all’interno di un valore assoluto:
- L’equazione |A(x)| = a non ha soluzione se a < 0 , altrimenti si risolve ponendo A(x) = ± a. (es |3x| = -1 non ammette soluzioni; |3x| = 1 -> x = ± 1/3)
- La disequazione |A(x)| < k , con k > 0, è equivalente a −k < A(x) < k , ossia al sistema:
A(x)>−k
A(x)<k
Esempio:
|x − 2| < 5 è equivalente a − 5 < x − 2 < 5 , ossia:
x− 2 > − 5 –> x >− 3 ; x−2 < 5 –> x < 7
soluzione: −3 < x < 7
- Le soluzioni della disequazione |A(x)| > k , con k > 0, sono date dall’unione delle soluzioni di A(x)<−k e di A(x)> k .
Esempio:
|x − 6| > 1 è equivalente all’unione delle disequazioni x − 6 < −1 ∨ x − 6 >1,
ossia x < 5 ∨ x > 7.