1.1 Gli insiemi

1.1 Gli insiemi

Si definisce ‘insieme‘ un raggruppamento di elementi che si possono individuare con precisione.

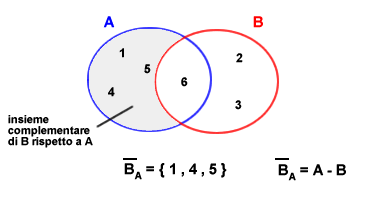
Si definisce ‘sottoinsieme’ di un insieme A un insieme B tale che ogni elemento di B appartiene anche ad A (come simbolo si usa ‘B c A’).

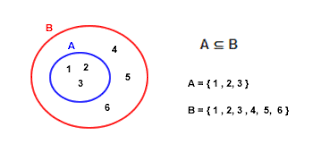
Passiamo ora a caratterizzarli:

Un insieme si dice:

• finito, quando è formato da un numero limitato di elementi;
• Infinito, quando il numero di elementi è illimitato; 
• vuoto, se non ha elementi.

Un sottoinsieme B di un insieme A si dice:

• proprio, se B è sottoinsieme di A ma B non coincide con A. 
• improprio, se B è l’insieme vuoto oppure B è un sottoinsieme di A tale che ogni elemento di A appartiene anche a B.

E’ possibile rappresentare un insieme in diversi modi:

• Elencazione -> scrivendo una lettera maiuscola che indica il nome dell’insieme, seguita dal segno uguale e di seguito si scrivono all’interno di parentesi graffe gli elementi, separati da una virgola o da punto e virgola.    Esempio:  A={3,5,7,9}.
• Caratteristica -> tra le parentesi graffe si indica la proprietà che accomuna tutti gli elementi. Esempio: l’insieme dei numeri naturali minori di 10 si indica con A : {x C N | x è minore di 10 }.
• Diagramma di Elurelo-Venn -> racchiudendo con una linea chiusa gli elementi indicati da un punto e un nome.

Inoltre, gli insiemi si possono anche relazionare, vediamo nel dettaglio:

• L’intersezione di due insiemi A e B è l’insieme C formato dagli elementi che si trovano sia in A sia in B; si scrive C= A ∩ B. Per esempio: A={a, e, i, o, u}, B={a, b, c, d, e, f, g} allora A ∩ B = {a,e}
• L’unione di due insiemi A e B è l’insieme C formato dagli elementi che appartengono ad A e anche a B (se ripetuti vanno presi una sola volta), si scrive C= A U B. Per esempio, A={a, e, i, o, u}, B={a, b, c, d,e, f, g} allora A U B={a,b,c,d,e,f,g,i,o,u}.

• La differenza di due insiemi A e B è l’insieme C costituito dagli elementi di A che non appartengono a B, in simboli C=A-B oppure C=A\B. Per esempio, A={a, e, i, o, u}, B={a, b, c, d,e, f, g} allora A – B= {i,o,u}.

• Due insiemi si dicono disgiunti se la loro intersezione è vuota. 

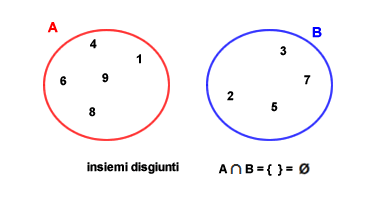
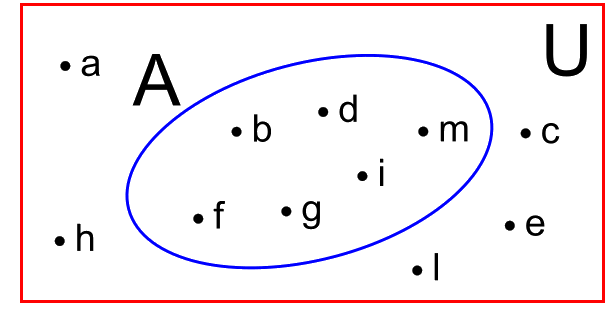
• L’insieme ambiente o universo è un insieme che contiene la totalità degli elementi.

In generale, dato un insieme A, l’insieme ambiente è un insieme che contiene A. Per esempio, se A è l’insieme dei numeri naturali multipli di 3, l’insieme universo può essere l’insieme di tutti i numeri naturali; se A è l’insieme delle vocali dell’alfabeto italiano, l’insieme universo può essere l’insieme di tutte le lettere dell’alfabeto italiano. 

©Youmath

• L’insieme complementare di B rispetto all’insieme U, scelto come insieme universo, è l’insieme costituito da tutti gli elementi di A che non appartengono a B. Per esempio, B={a, e, i}, U = {vocali} -> complementare di B (non B, solitamente s’indica come ‘B barrato’) B={o, u}