1.2 Proporzioni e Percentuale
Si definisce proporzione un’uguaglianza fra due rapporti. In termini matematici si scrive:
a:b=c:d, o ,equivalentemente, a/b = c/d
[Si legge “a sta a b come c sta a d”]
I termini a e d si dicono estremi, i termini b e c si dicono medi. Inoltre i termini a e c sono anche detti antecedenti, mentre b e d sono detti conseguenti, come mostrato nel seguente esempio:
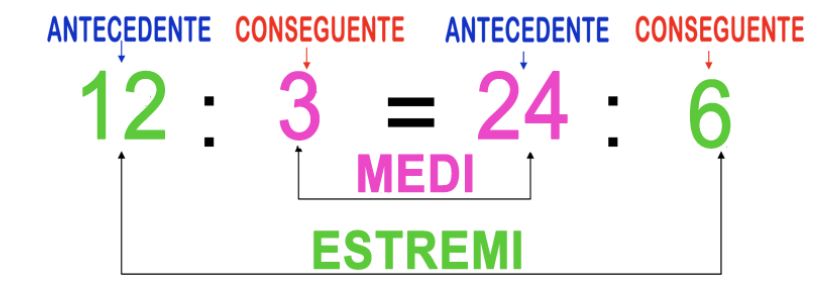
©Crediti: internet
Affinché la proporzione abbia senso, deve risultare b, d ≠ 0 (dal momento che il denominatore di una frazione dev’essere diverso da 0).
Diverse sono le proprietà di una proporzione, analizziamole nel dettaglio e con esempi:
– Proprietà fondamentale: in una proporzione il prodotto dei medi è uguale al prodotto degli estremi.
Se a:b=c:d allora a⋅d = b⋅c (es. 4:5 = 8:10 -> 4*10=40=5*8)
– Proprietà del comporre: In una proporzione la somma fra il primo e il secondo termine sta al primo (o al secondo), come la somma fra il terzo e il quarto termine sta al terzo (o al quarto).
Se a:b = c:d allora (a+b):a = (c+d):c e (a+b):b = (c+d):d, purché a,c ≠ 0 per la prima, b,d ≠ 0 per la seconda. (es. 4:5 = 8:10 -> (4+5):4=(8+10):8 -> 9:4=18:8)
– Proprietà dello scomporre. In una proporzione la differenza fra il primo termine e il secondo sta al primo (o al secondo), come la differenza fra il terzo e il quarto termine sta al terzo (o al quarto).
Se a:b = c:d allora (a−b):a = (c−d):c e (a−b):b = (c−d):d, purché a,c ≠ 0 per la prima, b,d ≠ 0 per la seconda. (es. 5:4 = 10:8 -> (5-4):4=(10-8):8 -> 1:4=2:8)
– Proprietà del permutare. Scambiando fra loro i medi e gli estremi di una proporzione si ottiene ancora una proporzione.
Se a:b=c:d allora a:c=b:d e d:b=c:a (es. 4:5 = 8:10 -> 4:8 = 5:10)
– Proprietà dell’invertire. Data una proporzione, è ancora una proporzione valida quella ottenuta scambiando ogni antecedente con il proprio conseguente.
Se a:b=c:d allora b:a=d:c (es. 4:5 = 8:10 -> 5:4 = 10:8)
Ma come si risolve una proporzione? Vediamolo subito!
Per rispondere a questa domanda bisogna introdurre il concetto di:
– Quarto proporzionale -> è il quarto elemento di una proporzione e si ricava nel seguente modo a:b=c:x ⇒ x=b⋅c / a (es. 4:5 = 8:10 -> 10 = 8*5/4)
– Terzo proporzionale -> è il terzo elemento di una proporzione e si ricava nel seguente modo a:b=x:c ⇒ x=a⋅c /b (es. 4:5 = 8:10 -> 8 = 10*4/5)
(In generale se l’elemento incognito è un medio occorre moltiplicare gli estremi e dividere per l’altro medio. Viceversa se l’incognita è un estremo si moltiplicano i medi e si divide per l’altro estremo)
Invece il Medio proporzionale è l’elemento medio della proporzione, nel caso in cui i due elementi medi siano uguali, si ricava nel seguente modo:
a:x=x:b ⇒ x=√ a⋅b (es. 3:6 = 6:12 -> 6 = √12*3 = √36)
Analizzato nei suoi sviluppi matematici il concetto di Proporzione, sviluppiamo ora il concetto di Percentuale (%).

©DINOS ENGLISH
Una percentuale è un rapporto tra due grandezze a e b espresso in centesimi. Per calcolare la percentuale sarà sufficiente svolgere questa formula:
Valore = (Numero ⋅ Percentuale) / 100
Dove:
Il Numero è il valore di riferimento di cui si intende calcolare la percentuale e rappresenta il totale.
La Percentuale è un numero ,compreso tra lo 0 ed il 100, rappresentativo della parte di totale di cui vogliamo calcolarci il valore percentuale.
Il Valore è la percentuale calcolata.
Ecco alcuni esempi:
- 20% di 70 -> 20*70/100 = 1400/100 = 14
- 16% di 83 -> 16*83/100 = 1328/100 = 13,28
Quiz esempio:
Dato un capo di abbigliamento di 40€ , ricavare l’importo finale sottraendo il 20% di sconto.
Si calcola il 20% di 40, e cioè si moltiplica 20 per 40 e si divide tutto per 100: (40 ⋅ 20) / 100 = 8
Una volta ottenuto il valore dello sconto (8 euro) bisognerà sottrarlo alla cifra di partenza.
40 – 8 = 32, che corrisponde all’importo finale, ottenuto mediante lo sconto del 20%.