1.4 Radicali e Logaritmi
Si definisce numero razionale un qualsiasi numero che può essere scritto sotto forma di frazione.
Sono quindi numeri razionali:
- Tutti i numeri interi
- Tutti i numeri decimali limitati
- Tutti i numeri decimali periodici
Si dice invece numero irrazionale ogni numero che non può essere scritto sotto forma di frazione. Appartengono all’insieme dei numeri reali sia i numeri razionali che quelli irrazionali.
Definiamo nel dettaglio i vari membri di questa particolare tipologia di numeri: sia ‘a’ un numero reale relativo qualunque ed ‘n’ un numero intero positivo; se esiste un numero reale relativo x che elevato ad n dà a (cioè tale che x^n =a) allora si dice che ‘x’ è radice algebrica ennesima di ‘a’.
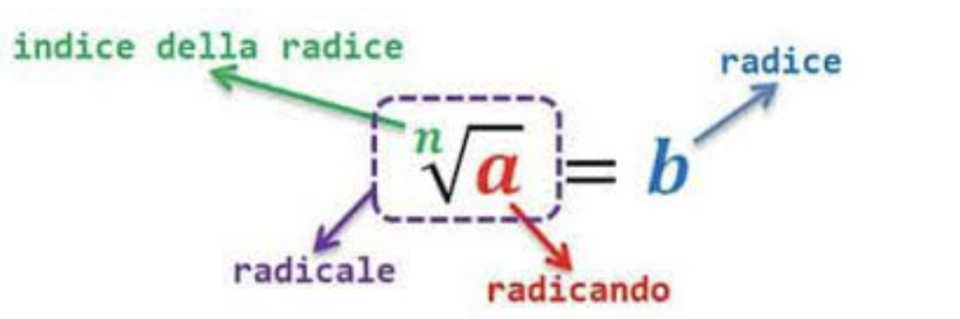
©SOS matematica
Tale simbolo, detto ‘radicale’, rappresentato in figura si legge in maniera completa: “b è la radice ennesima di a”. In particolare:
- a è il radicando
- b è la radice
- n è l’indice della radice
- √ è segno della radice
Se l’indice della radice n = 2, cioè quando si tratta di una radice quadrata si è soliti omettere l’indice. Quindi la radice algebrica n-esima di a (numero positivo o negativo) è quel numero (positivo o negativo) la cui potenza n-esima dà il numero ‘a’. Facendo un breve richiamo sulle proprietà delle potenze abbiamo:
- Se a>0 allora a^n>0 sia che n sia pari o dispari (es. 3^(-1) = 1/3; 3^2=9)
- Se a<0 allora a^n>0 se n è pari e a^n<0 se n è dispari (es. (-3)^(-1) = -1/3; (-3)^2=9)
Ricordando che se a^n = b allora a = radice ennesima di b -> l’operazione di estrazione di radice altro non è che l’operazione inversa rispetto a quella di elevamento a potenza; si deduce da quanto abbiamo visto dalle proprietà delle potenze che la radice algebrica di un numero a (positivo o negativo) è tale che:
- Quando l’indice di radice ‘n’ è pari allora: 1) se il radicando ‘a’ è positivo (cioè se a > 0) allora ammette come soluzioni 2 valori che hanno lo stesso Valore Assoluto (ricordiamo che il valore assoluto o modulo di un numero relativo ‘a’, indicato con |a|, è il numero stesso privato del segno) ma segno opposto cioè: √a=+-b; 2) se il radicando ‘a’ è negativo (cioè se a < 0) allora non ammette alcuna soluzione nel campo dei numeri reali, perchè nessun numero elevato al quadrato (o a 4,6,8,…) dà come risultato un numero negativo; (es.√4 = +2, -2; √-4 non esiste nell’insieme dei numeri reali)
- Quando l’indice di radice ‘n’ è dispari allora: 1) se il radicando ‘a’ è positivo (cioè se a > 0) allora ammette come soluzione un unico valore positivo; 2) se il radicando ‘a’ è negativo (cioè se a < 0) allora ammette come soluzione un unico valore negativo. (es. 3√27 = 3; 3√-27 = -3)
A questo punto passiamo a tutte quelle tecniche che ci consentono di semplificare i calcoli coi radicali, di svilupparli e calcolarli.
Proprietà invariantiva dei radicali: dato un radicale, moltiplicando l’indice del radicale e l’esponente del radicando per uno stesso numero naturale diverso da 0, si ottiene un radicale equivalente. È possibile ottenere un radicale equivalente anche dividendo indice ed esponente per un loro divisore comune.
(Applicando la proprietà invariantiva è possibile semplificare un radicale oppure ridurre allo stesso indice più radicali)
(es.√16^3 = 4√16^6, ovvero si è moltiplicato per 2 sia l’indice del radicale (2*2=4) che l’esponente del radicando (3*2=6))
Il prodotto di due radicali con lo stesso indice è un radicale che ha lo stesso indice e per radicando il prodotto dei radicandi.
es. (indice pari a 2) : √3*√7=√21
Se i radicali hanno indice diverso, per moltiplicarli è sufficiente ridurli al loro minimo comune indice.
es. (indice minimo comune è 6) : 3√4 * 2√5= 6√4^2 * 6√5^3 = 6√16 * 6√125 = 6√2000 (si è moltiplicato per 2 l’esponente di 4, ovvero 1*2 = 2, e l’indice del radicale, ovvero 3*2, idem per il secondo radicale, ma con moltiplicazione per 3)
Un’ulteriore considerazione che si può fare per semplificare ancora di più le espressioni coi radicali è il fatto che un fattore del radicando, scritto sotto forma di potenza con base non negativa, può essere portato fuori dal segno di radice, se il suo esponente m è maggiore o uguale all’indice n della radice. Il fattore esterno ha per esponente il quoziente della divisione fra m e n, quello interno ha per esponente il resto della divisione. (es. 4√5^6 = 4√5^4*5^2 = 5*4√5^2)
Un’altra tecnica che consente lo sviluppo e il calcolo dei radicali è la cosiddetta razionalizzazione, ovvero è possibile razionalizzare il denominatore (in cui compaiono radicali) di una frazione, moltiplicando numeratore e denominatore per un opportuno identico fattore diverso da 0.
(es. : 2/√2 = 2/√2*√2/√2 = 2*√2/√4 = 2*√2/2 = √2)
Se il denominatore di una frazione è la somma o la differenza di due termini, dei quali almeno uno è un radicale quadratico: es : 8/√7+√2, si moltiplica numeratore e denominatore per la differenza √7- √2. , in modo da applicare il prodotto notevole (a+b)(a−b)=a^2 −b^2, e dunque: 8/√7+√2 * (√7- √2/√7-√2) = 8*(√7-√2)/(7-2) = 8/5 * (√7-√2)
A questo punto, passiamo ad analizzare i LOGARITMI:
Dati due numeri reali positivi ‘a’ e ‘b’, con a≠1, il logaritmo in base ‘a’ di ‘b’, è l’esponente da assegnare ad ‘a’ per ottenere ‘b’ : x = loga(b) -> a^x = b (es. 3^2 = 9 -> 2 = log3(9)).
I logaritmi godono di una serie di proprietà, ovvero regole di calcolo, che permettono di semplificare notevolmente le espressioni logaritmiche. Tali proprietà valgono per qualunque scelta della base del log (‘a’ nell’espressione) MA base ed argomento devono essere presi maggiori strettamente di zero e la base anche diversa da 1.
Nella seguente immagine sono riportate le proprietà del prodotto, del rapporto e della moltiplicazione-esponente:
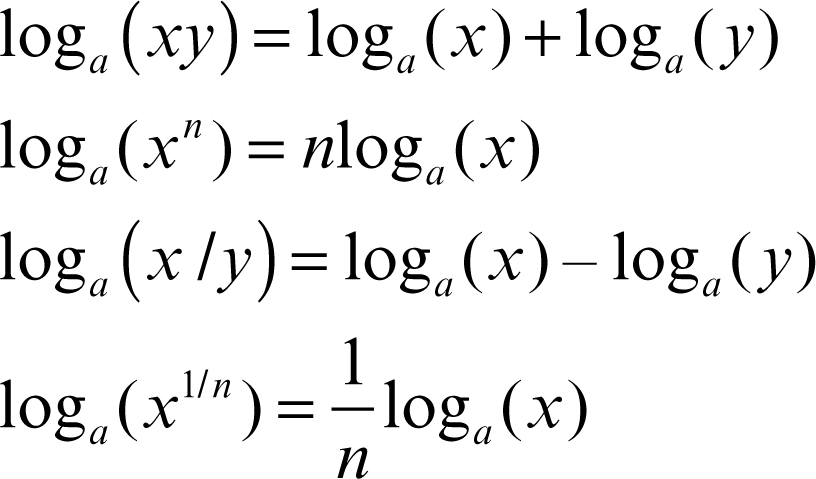
©Treccani
Es. log3(3*9) = log3(3) + log3(9) = 1 + log3(3*3) = 1 + log3(3) + log3(3) = 1 + 1 + 1 = 3
Es. log2(16/8) = log2(16) – log2(8) = log2(2^4) – log2(2^3) = 4*log2(2) – 3log2(2) = 4-3 = 1
Es. log3(3*9) = log3(27) = log3(3^3) = 3*log3(3) = 3*1 = 3
Oltre alle formule legate al logaritmo di un prodotto e di un rapporto, vi è anche la formula che consente il cambiamento di base: talvolta nei calcoli è conveniente scrivere il log con differente base per poter continuare a svolgere l’esercizio e applicare le formule note. Questa nuova base deve essere positiva e diversa da 1:
loga(b) = logc(b)/logc(a) -> es. log4(16) = log2(16)/log2(4) = log2(2^4)/log2(2^2) = 4log2(2)/2log2(2) = 2