1.9 Calcolo combinatorio

1.9 Calcolo combinatorio

Il calcolo combinatorio studia il numero di raggruppamenti distinti che, secondo un determinato criterio, si possono formare con gli elementi di un certo insieme. Prima di addentrarci nelle varie casistiche di calcolo combinatorio, cominciamo con l’introdurre un elemento che tornerà spesso e utile nei calcoli:

Il fattoriale di un numero n si indica con n! ed è uguale al prodotto di n numeri naturali decrescenti a partire da n:

n! = n(n – 1)(n – 2)(n – 3) …

Ad esempio 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720

Se parliamo di calcolo combinatorio dobbiamo distinguere chiaramente le permutazioni, combinazioni e disposizioni.

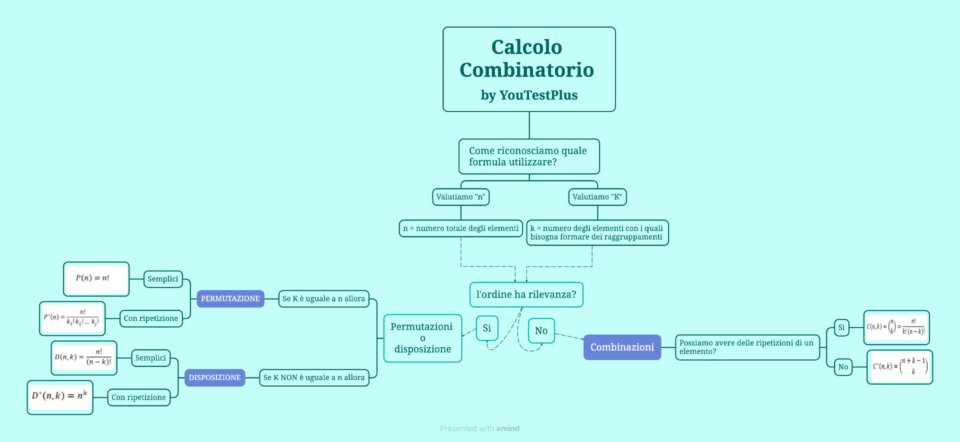
Le permutazioni, le combinazioni e le disposizioni sono concetti fondamentali nel calcolo combinatorio, e ognuno di essi rappresenta un modo diverso di organizzare gli elementi di un insieme. Diamo delle definizioni per ciascuno di questi concetti:

1. Permutazioni: Le permutazioni sono ordini diversi in cui gli elementi di un insieme possono essere disposti. L’ordine è fondamentale. Ad esempio, se abbiamo un insieme di n elementi, ci sono n! (n fattoriale) modi distinti di organizzare gli elementi in permutazioni. La formula per il calcolo delle permutazioni è: P(n)=n!; dove n! rappresenta il fattoriale di n, ovvero il prodotto di tutti gli interi positivi da 1 a n.
2. Combinazioni: Le combinazioni sono sottoinsiemi di elementi di un insieme, senza considerare l’ordine. In altre parole, si tratta di selezioni di elementi senza considerare la sequenza in cui vengono scelti. Ad esempio, se abbiamo un insieme di n elementi e vogliamo selezionare k elementi da esso, il numero di combinazioni possibili è dato dai coefficienti binomiali, definiti come: (n_k)= [n! / k!(n−k)! ]; dove (n _k) rappresenta il numero di combinazioni di n elementi presi k alla volta.
3. Disposizioni: Le disposizioni sono simili alle permutazioni, ma coinvolgono solo un sottoinsieme di elementi dell’insieme di partenza. Tuttavia, a differenza delle combinazioni, l’ordine è ancora importante. Quindi, in una disposizione, gli elementi sono selezionati e disposti in un ordine specifico. Se abbiamo un insieme di n elementi e vogliamo selezionare k elementi e disporli in un ordine specifico, il numero di disposizioni possibili è dato da: D(n,k) = [n! / (n−k)!]; dove D(n,k) rappresenta il numero di disposizioni di n elementi presi k alla volta.

Vediamoli ora leggermente più da vicino:

Si chiamano permutazioni semplici di n oggetti distinti le disposizioni semplici degli n oggetti dati di classe k = n, si indicano con P:

P_n = n!

Le permutazioni semplici di n oggetti distinti sono tutti i possibili raggruppamenti contenenti la totalità degli n oggetti dati e che differiscono soltanto per l’ordine con cui gli elementi sono disposti. Ad esempio, per conoscere quante parole, anche prive di significato, si possono formare con le lettere a, p, e, è sufficiente calcolare le disposizioni semplici delle tre lettere prese a tre a tre.

Esempi:

Quanti sono gli anagrammi della parola “NAPOLI”?
Dato che parliamo di una permutazioni semplice, dunque di una permutazione in cui non sono presenti ripetizioni di lettere, abbiamo che il numero di anagrammi della parola NAPOLI è uguale P_n = n! -> P₆ = 6! -> 6*5*4*3*2*1* = 720.

Quanti sono gli anagrammi della parola “FAENZA”?
In questo caso , dato che parliamo di una permutazione con ripetizione (la lettera “A” si ripete due volte) avremo che la formula sarà: n = (6! / 2!) = 6*5*4*3= 360

Vediamo ora un esempio rappresentando ‘ad albero’:

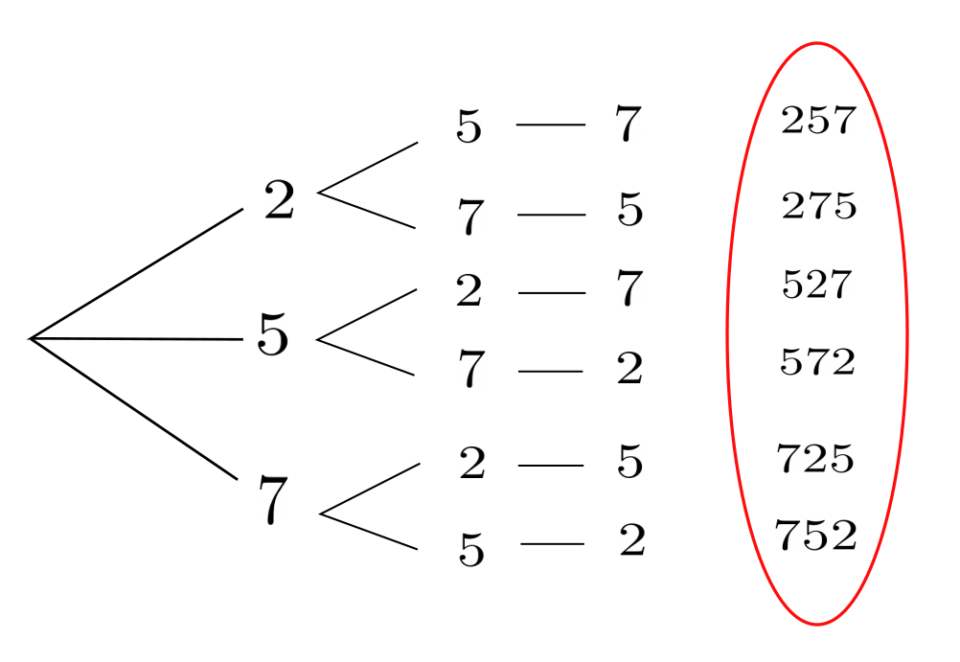
©Formuliamo

Dati n oggetti distinti e indicato con k un numero intero positivo minore o uguale ad n, si chiamano disposizioni semplici degli n oggetti, presi a k a k (o di classe k), tutti i possibili raggruppamenti che si possono formare con gli n oggetti dati, che contengono ognuno k elementi, in modo che ciascuno di essi differisce dagli altri o per un elemento diverso o per l’ordine in cui gli oggetti sono disposti. Si indica con il simbolo Dn,k.

Per comprendere facilmente il concetto si consideri un insieme formato da quattro elementi A = {a, b, c, d}. Volendo disporre gli elementi di A a due a due (classe k = 2), è sufficiente associare ad ogni elemento di A, ad esempio a, i rimanenti elementi b, c, d. Un diagramma ad albero favorisce l’individuazione di tali coppie. In generale, si può dimostrare che la disposizione di n oggetti di classe k è uguale al prodotto di k numeri naturali consecutivi e decrescenti a partire da n: 

Dn,k = n(n – 1)(n – 2)(n – 3) … (n – k + 1)

Con l’utilizzo del fattoriale, si può anche scrivere:

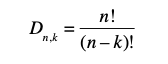
Esempio:

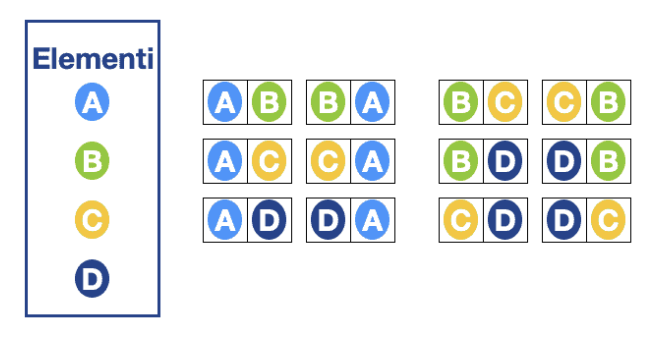
Dati 4 elementi, A, B, C, D (n=4) -> per dividerli in raggruppamenti di 2 elementi (k=2) -> otteniamo 12 blocchi, difatti: 4!/(4-2)! = 4!/2! = 4*3 = 12

©Adrianogilardone

Nella formazione dei raggruppamenti sin qui esaminati (permutazioni e disposizioni), l’ordine degli oggetti assume rilevanza.

Si consideri ora una ulteriore tipologia di raggruppamento, ovvero quella delle combinazioni semplici, caratterizzata dal fatto che non si tiene conto dell’ordine degli n oggetti con i quali si effettua il raggruppamento medesimo. In generale, dati n oggetti distinti e indicando con k un numero intero positivo minore o uguale ad n, si chiamano combinazioni semplici di questi n oggetti, presi a k a k (o di classe k), tutti i possibili raggruppamenti che si possono formare con gli oggetti dati in modo che uno stesso oggetto non può figurare più volte in un raggruppamento, e due raggruppamenti sono da considerarsi diversi solo quando differiscono almeno per un oggetto.

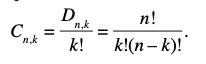
Esempio:

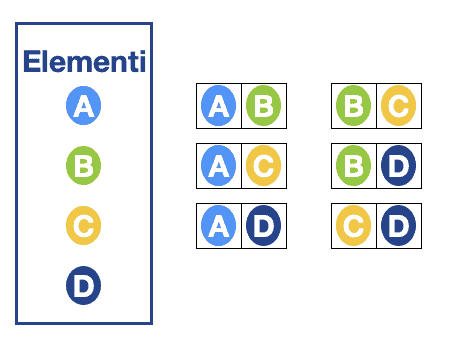
Dati 4 elementi, A, B, C, D (n=4) , e k = 2 -> otteniamo 6 blocchi, difatti: 4!/(2!(4-2)!) = 4!/2!2! = 4*3*2/2*2 = 6

©Adrianogilardone

A questo punto analizziamo i casi con ripetizione:

Dati n oggetti distinti e indicato con k un numero intero positivo qualsiasi (anche maggiore di n), si chiamano disposizioni con ripetizione di questi n oggetti, presi a k a k (di classe k), tutti i possibili raggruppamenti che si possono formare con gli n oggetti dati, in modo che valgano le seguenti proprietà:

• in ogni raggruppamento uno stesso oggetto può figurare sino ad un massimo di k volte;

• due raggruppamenti sono considerati distinti quando uno di essi contiene almeno un oggetto che non figura nell’altro; oppure contengono gli stessi oggetti, ma almeno uno di essi è ripetuto un numero diverso di volte; oppure, pur contenendo gli stessi oggetti, ripetuti lo stesso numero di volte, questi differiscono per l’ordine con cui sono disposti.

Il numero delle disposizioni con ripetizione di n oggetti distinti, presi a k a k, è

D′ _n,k =n^k

Esempio:

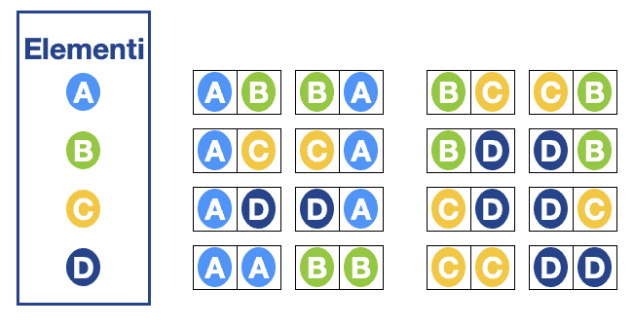
Dati 4 elementi, A, B, C, D (n=4) , e k = 2 -> otteniamo 16 blocchi, difatti: 2^4 = 16

©Adrianogilardone

Il numero delle permutazioni con ripetizione di n elementi, m dei quali uguali tra loro, è uguale al quoziente fra il numero delle permutazioni semplici degli n elementi e il fattoriale di m.

Se poi degli n elementi dati risulta che m siano uguali tra loro, q siano uguali tra loro con

m + q … n, si ha

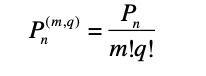
Esempio:

Dati 3 elementi, A, B, B (n=3) , e k = 3 -> otteniamo 3 blocchi, difatti: 3!/2!1! = 3*2/2 = 3

©Adrianogilardone

Nelle combinazioni con ripetizione, uno stesso oggetto può figurare anche più volte in ciascun raggruppamento e non è rilevante l’ordine degli oggetti. In particolare, si chiamano combinazioni con ripetizione di n oggetti distinti di classe k tutti i raggruppamenti contenenti k di questi oggetti in modo che in essi ciascun oggetto possa trovarsi al massimo k volte e in modo che due raggruppamenti differiscano tra loro almeno per un oggetto, oppure quando, contenendo gli stessi oggetti, questi non compaiono due volte in ugual numero.

La formula generale è la seguente:

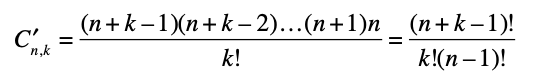
Esempio:

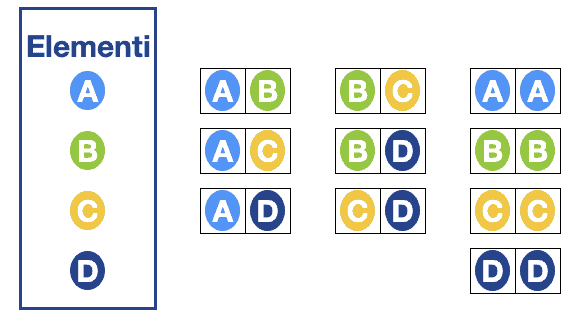
Dati 4 elementi, A, B, C, D (n=4) , e k = 2 -> otteniamo 10 blocchi, difatti: (4+2-1)!/2!(4-1)! = 5!/2!3! = 5*4*3*2/2*3*2 = 10

©Adrianogilardone